Graph Database Concepts

The graph database stores and manages objects of a real model in graph form.
A relation (edge) exists between objects (vertices), and a group of similar vertices can be expressed as a group (label).
As vertices and edges have data (properties), they can be called Property Graph Models as well.

Let’s take a closer look at the components of this graph data model.
The following example shows components of a graph:

Vertices

Vertices are the most basic elements in the graph data model. They represent entities in the real world and have properties.

A graph has vertices and edges as the base units. In AgensGraph, both vertices and edges may contain Properties. While entities are usually represented by vertices, they may be indicated using edges in some cases. Unlike edges and properties, vertices may have zero or multiple label values.

The simplest form of a graph consists of a single vertex. A vertex can have zero or more properties.

The next step is to construct a graph with multiple vertices. Add two or more vertices to the graph of the previous step and add one or more properties to the existing vertex.

Edges

Edges connect vertices. When two vertices are connected via en edge and each vertex plays as start vertex or end vertex depending on the direction of the edge. Like vertices, edges have properties.
The edges between vertices play an important role in the graph database, especially when you search for linked data.
With edges, you may make vertices into a variety of data structures, such as lists, trees, maps, and composite entities. By adding edges to the example we are building, we can represent more meaningful data.

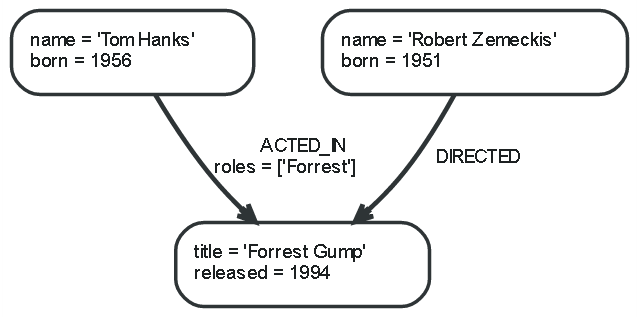
In the example, ACTED_IN and DIRECTEDare used as edge types. The ACTED_IN property, Roles, stores the value of array type.

The ACTED_IN edge has the Tom Hanks vertex as start vertex and the Forrest Gump vertex as end vertex. In other words, we can say that the Tom Hanks vertex has an outgoing edge and the Forrest Gump vertex has an incoming edge.

If there is an edge in a single direction, you do not have to duplicate the edge and add it in the opposite direction; this is related to the graph traversal or performance.

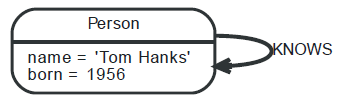
Edges are always directional, but they may ignore directionality if it is not needed in your application. The diagram below shows a vertex having an edge pointing to itself.

All edges are recommended to have an edge type to perform the graph traversal in a more efficient manner.

Properties

Both vertices and edges may have properties. Properties are attribute values, and each attribute name should be defined only as a string type.

The available data types for property values are:

• Numeric type

• String type

• Boolean type

• List type (a collection of various data types)

NULL values cannot be used as property values. If NULL is entered, the property itself is assumed to be absent. NULL values, however, can be used in List.

Type	Description	Value range
boolean		true/false
byte	8-bit integer	-128 to 127, inclusive
short	16-bit integer	-32768 to 32767, inclusive
int	32-bit integer	-2147483648 to 2147483647, inclusive
long	64-bit integer	-9223372036854775808 to 9223372036854775807, inclusive
float	variable-precision, inexact	15 decimal digits precision
char	16-bit unsigned integers representing Unicode characters	u0000 to uffff (0 to 65535)
String	sequence of Unicode characters	infinite

Labels

You may define the roles or types of vertices or edges using labels. Vertices or edges with similar characteristics can be grouped and the name of such a group can be defined, which is called a “label.” That is, all vertices or edges with similar labels belong to the same group.

Database query statements can be performed only on the group (not the entire graph) using labels, which is helpful for a more efficient querying.

Using labels for vertices is optional, and each vertex may have zero or only one label.

Labels can also be used to define constraints on properties or to add indexes.

You may also assign a label similar to a vertex to an edge. Unlike vertices, there is no edge without a label; all edges should have at least one label.

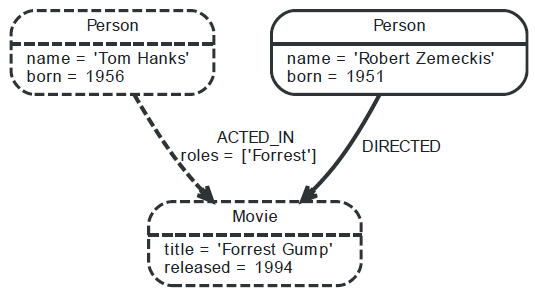
Let us add Person and Movie labels to the existing example graph.

Label names

Label names can be expressed using letters and numbers, all converted to lowercase letters.

Labels stores a unique id of int type, which means that the database may contain up to 2^16-1(65535) labels.

Traversal

Traversal is to traverse paths while exploring a graph to answer the requested query. Traversal is a process of searching for the relevant vertices from start vertex to find the answer to the requested query. In other words, it refers to following the vertices that are traversing the graph and the derived edges according to a specific rule.

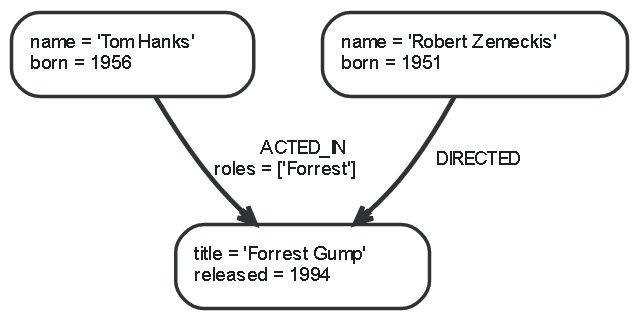
In the examples illustrated so far, we try to find a movie featured by Tom Hanks. Starting with the Tom Hanks vertex, you can traverse all the processes that end at the vertex of Forrest Gump along the ACTED_IN edge associated with it.

By using the traversal of cypher query statements and additional techniques in the graph database, you may derive better result data. For more information, see Cypher Query Language.

Paths

Paths are the result data of a query statement or traversal, which shows one or more vertices and the edges connected to them.

The path (traversal result data) from the previous example is as follows:

The length of the above path is 1. The shortest path length is 0, which is the case when a single vertex does not have edges.

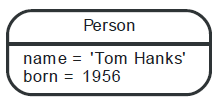
If the vertex has an edge pointing to itself, the length of path is 1.